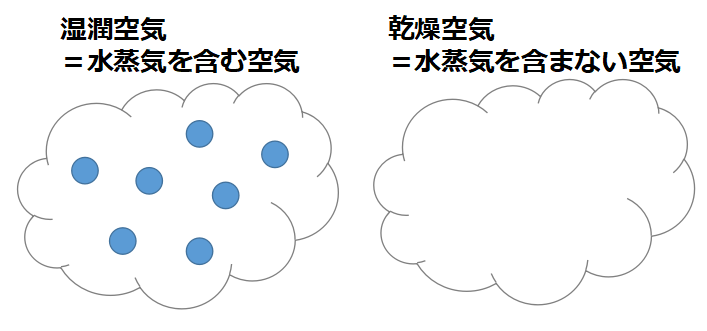
「ある湿潤空気に対して,同じ圧⼒,同じ(a)をもつ乾燥空気の温度を仮温度と定義することにより,湿潤空気の状態を表す式として,乾燥空気に対する状態⽅程式を⽤いることができる。ある気圧における湿潤空気の温度と仮温度とを⽐べると,仮温度の⽅が(b)。」
(a)は密度、(b)は高いが正解です。
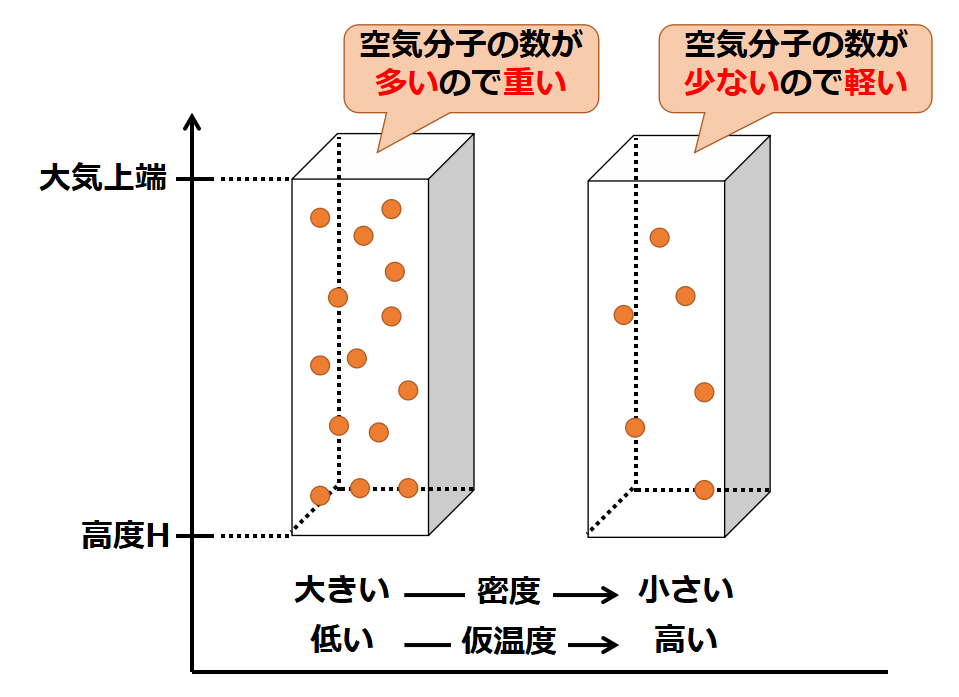
ある湿潤空気と、ある乾燥空気について、状態方程式PV=nRTの要素を考えます。
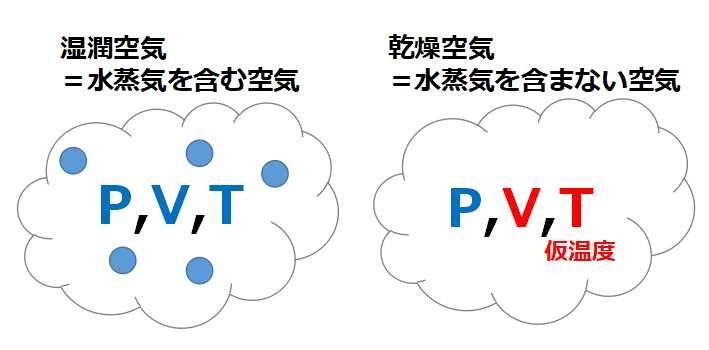
問題文より圧力Pは同じです。
また乾燥空気の温度は仮温度として定義されているので、T(仮温度)とします。そして湿潤空気の温度はTとします。
V(体積)については指示がないので、”同じ(a)”はV(体積)に関するものだと推測します。体積とは「物質の空間的な大きさ」です。
気体の体積とは「気体分子が飛び交っている空間の範囲」です。
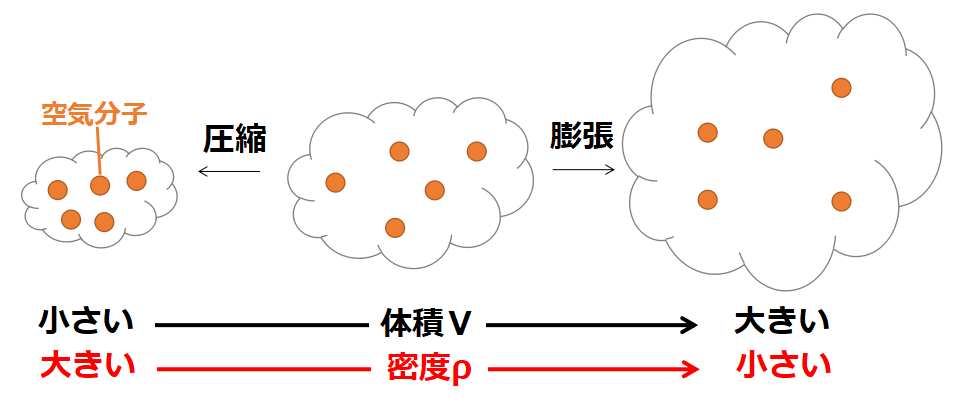
体積に占める空気分子の数は密度として表されます。
・空気が膨張すると体積が大きくなりますが、空気分子の数は変わりません。
よって密度が小さくなります。
・空気が圧縮すると体積が小さくなりますが、空気分子の数は変わりません。
よって密度が大きくなります。
この時点で(a)は比熱ではなく密度だと推測できます。
次に「湿潤空気の状態を表す式として,乾燥空気に対する状態⽅程式を⽤いることができる」とあるので、状態方程式PV=nRTを用いて表していこうと思いました。
しかし気体定数Rは乾燥空気と湿潤空気で異なるため、状態方程式で表そうとすると不明な要素が多くなって上手く表せません。
そこで仮温度とはどういうものなのかを考えます。
問題文より、仮温度は「ある湿潤空気に対して,同じ圧⼒,同じ密度をもつ乾燥空気の温度」と定義されます。
乾燥空気の構成成分は主に窒素(分子量28)と酸素(分子量32)です。
”湿潤空気=乾燥空気+水蒸気”なので、湿潤空気の構成成分は主に窒素(分子量28)と酸素(分子量32)と水分子(分子量18)です。
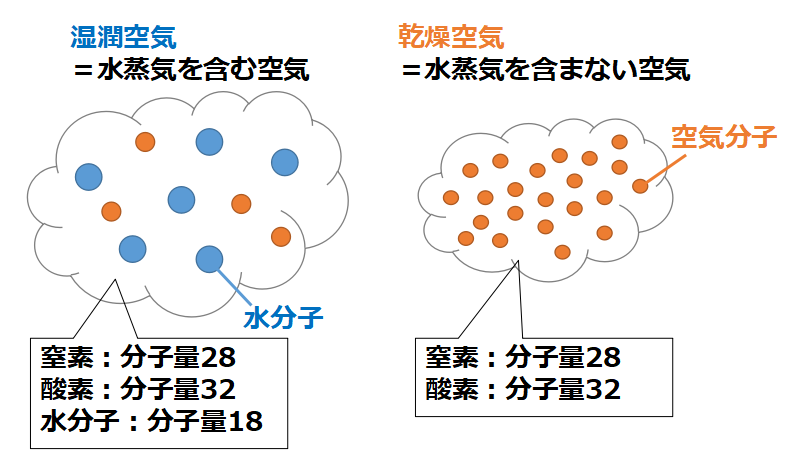
ここで圧力と温度が同じだと仮定すると、 分子量が小さい水分子を含む湿潤空気のほうが軽い(=密度が小さい)ことがわかります。
仮温度では湿潤空気と乾燥空気の密度が同じなので、乾燥空気の密度を小さくして、湿潤空気の密度と同じにする方法を考えます。
密度を小さくするには、体積を大きくすればよい(=空気を膨張させればよい)です。
空気を膨張させるには温度を高くすればよいので、以下のようになります。
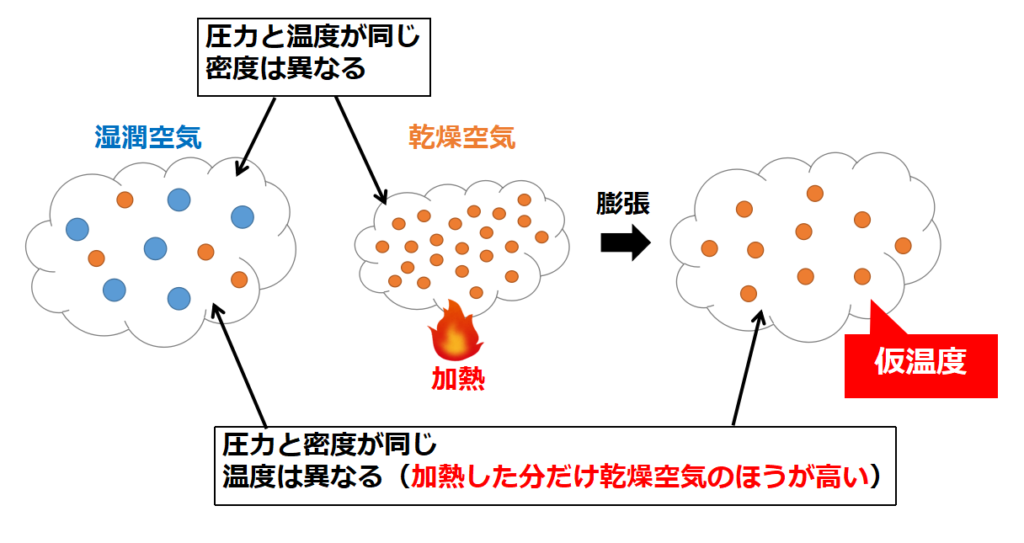
よって「ある湿潤空気に対して,同じ圧⼒,同じ密度をもつ乾燥空気」の温度(=仮温度)は、湿潤空気の温度よりも高くなります。
よって正解は「(a)密度」「(b)高い」です。