気温，気圧，相対湿度が，それぞれ27℃，1008hPa，50%の大気における，乾燥空気の分圧として最も適切なものを，下記の①~⑤の中から1つ選べ。ただし，水蒸気の気体定数を461 J kg-l K-l，27℃における飽和水蒸気密度を26 g m-3とする。
| ① | 1005hPa |
| ② | 1000hPa |
| ③ | 995hPa |
| ④ | 990hPa |
| ⑤ | 985hPa |
解説
大気中の乾燥空気の分圧を求める問題ですが、問題文には水蒸気に関するデータが与えられています。
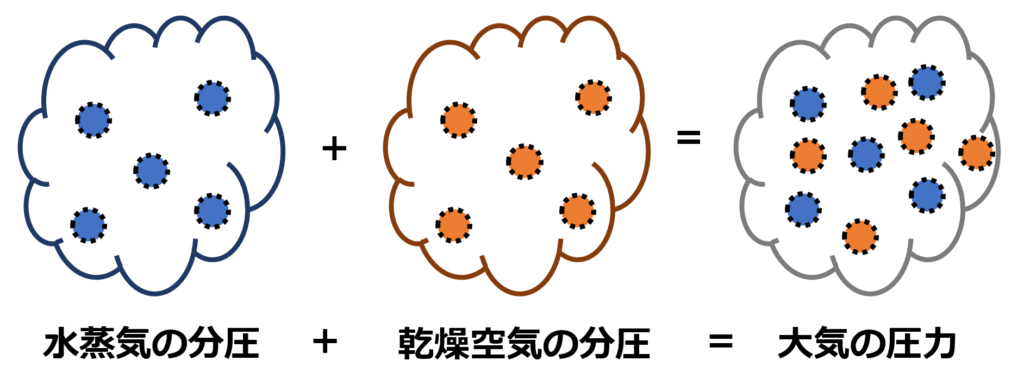
分圧は以下のように考えらえるので、最初に水蒸気の分圧を求めて、大気の圧力(1008hPa)から引いて、乾燥空気の分圧を求めていきます。
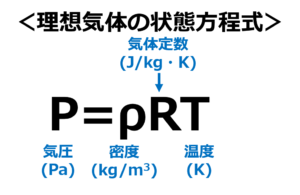
水蒸気の分圧を求めるためには、理想気体の状態方程式を使います。
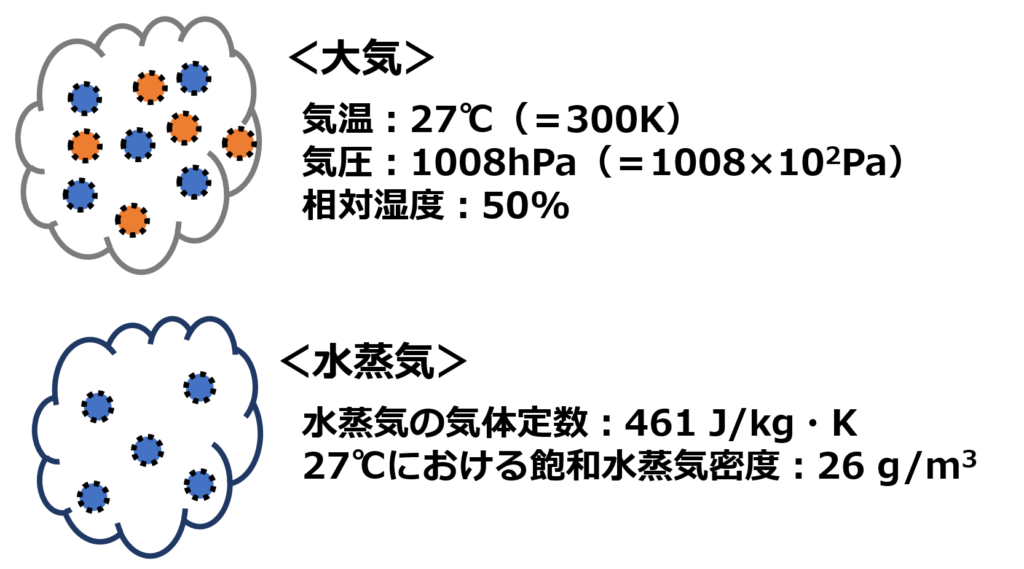
問題文より、大気と水蒸気の情報は以下の通りです。
ここから水蒸気の分圧(P)を求めていきます。
気体定数Rは461 J/kg・K、気温Tは300Kです。
密度ρに関しては「27℃における飽和水蒸気密度は26 g/m3」という情報があります。
問題文に「大気の相対湿度が50％」とあるので、単純に「ρ＝26」ではないことに気付くと良いと思います。
27℃の大気の場合、1m3あたり最大で26gの水蒸気を含むことができます。
今回は「大気の相対湿度が50％」なので、大気中には1m3あたり26g×50%=13gの水蒸気が含まれています。
よって水蒸気の分圧を求めるのに用いる密度ρは、13g/m3＝0.013kg/m3です。
以上より水蒸気の分圧(P)を計算すると、
P＝ρRT ＝ 0.013×461×300 ＝ 1797.9(Pa) ≒ 18(hPa)
となります。
大気の圧力は1008hPaなので、乾燥空気の分圧を求めると、
1008－18＝990hPa
となります。