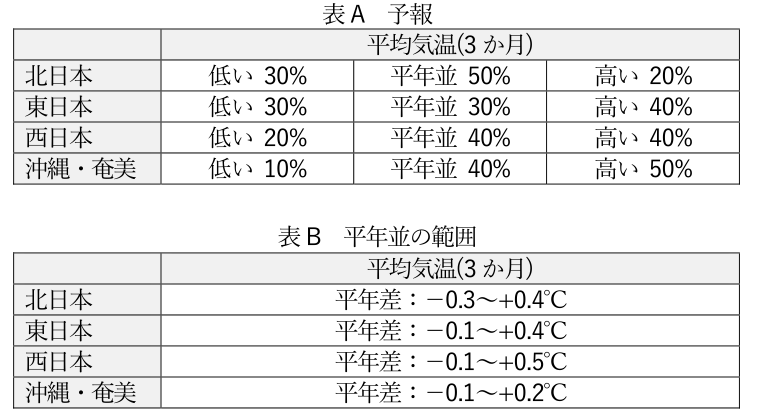
表Aは，3か⽉予報における3か⽉平均気温の予報であり，表Bは，この期間の平年並の範囲を表している。これらについて述べた次の⽂(a)〜(c)の正誤の組み合わせとして正しいものを，下記の①〜⑤の中から⼀つ選べ。ただし，平年並の範囲は，過去30年間（1981〜2010年）の出現率が，気温の低いほうから 33%〜67%をさし，これをその期間の平均値からの差で表している。
-
(a) 気温が「⾼い」になる可能性は，⻄⽇本のほうが東⽇本よりも⼤きい。
-
(b) 気温が平年差+0.2℃を上回る可能性は，沖縄・奄美のほうが⻄⽇本よりも⼤きい。
-
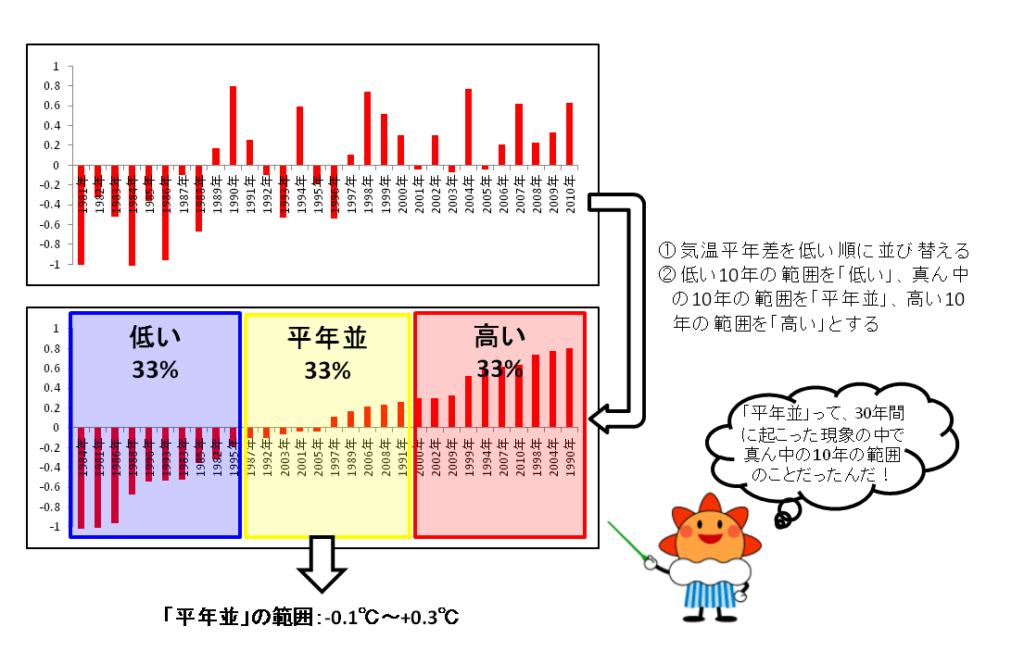
(c) 平年並の範囲を算出するデータの中に極端な⾼温の年があり，極端な低温の年はない場合，平年並の範囲は，東⽇本のように，平年差が正の範囲（東⽇本では0.4℃）のほうが負の範囲（東⽇本では0.1℃）よりも⼤きくなる。
| (a) | (b) | (c) | |
| ① | 正 | 正 | 誤 |
| ② | 正 | 誤 | 正 |
| ③ | 誤 | 正 | 正 |
| ④ | 誤 | 誤 | 正 |
| ⑤ | 誤 | 誤 | 誤 |
解説 (c)について
「平年並の範囲を算出するデータの中に極端な⾼温の年があり，極端な低温の年はない場合，平年並の範囲は，東⽇本のように，平年差が正の範囲(東⽇本では0.4℃)のほうが負の範囲(東⽇本では0.1℃)よりも⼤きくなる。」
これは誤です。
"平年並の範囲を算出するデータ"は2019年現在だと、1981年～2010年の30個のデータです。
「平年より高い/平年並み/平年より低い」を考えるときは、まず各年での「1981年～2010年の平均値からの差」を算出します。
算出した30個のデータを下図のように順番に並べて、高いほう30個の範囲が平年より高い、真ん中30個の範囲が平年並み、低いほう30個の範囲が平年より低いとなります。
個数で区切っているので、仮に極端な⾼温の年が1個だけあって、極端な低温の年はない場合でも、真ん中30個の平年並みの範囲に影響はありません。（下図参考）
※説明用に作ったグラフです。実際のデータではありません。