ハドレー循環の上層⾵のように⾚道から極向きに移動する空気塊を想定し，その運動について述べた次の⽂章の空欄(a)，(b)に⼊る適切な式と数値の組み合わせを，下記の①〜⑤の中から1つ選べ。ただし，⾚道における地球の⾃転速度を470m/s，cos30°=0.87，1/cos30°=1.15 とする。
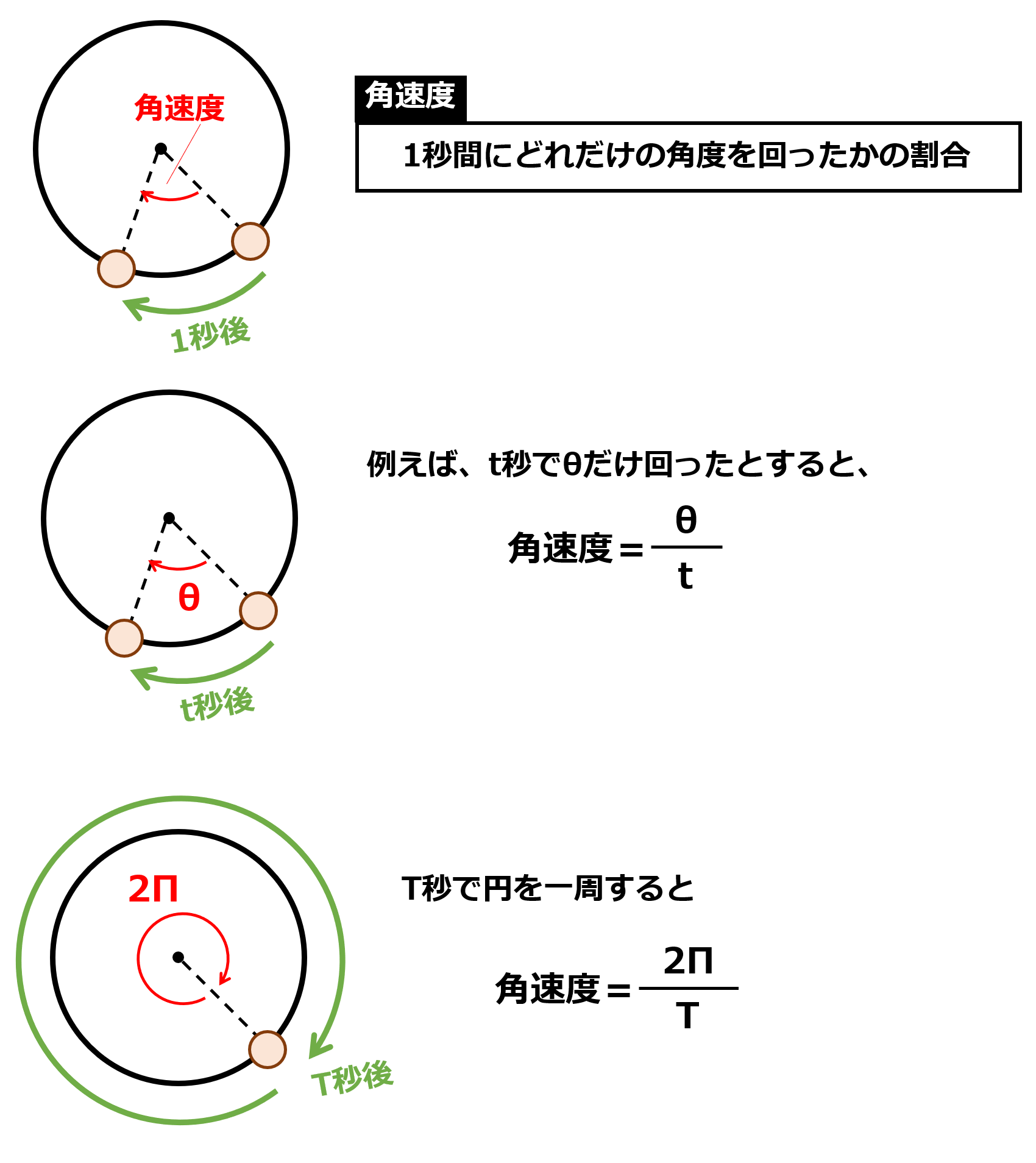
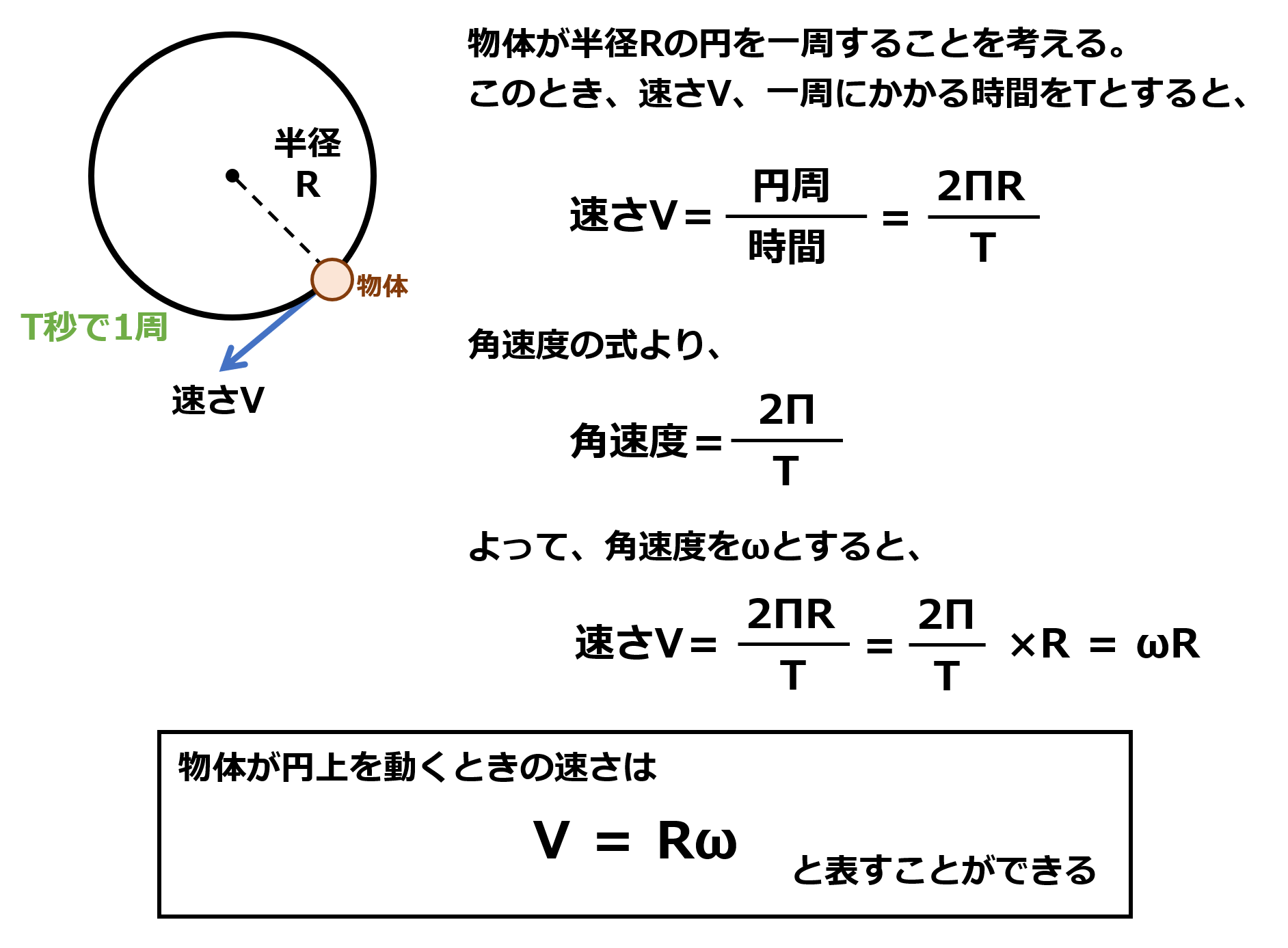
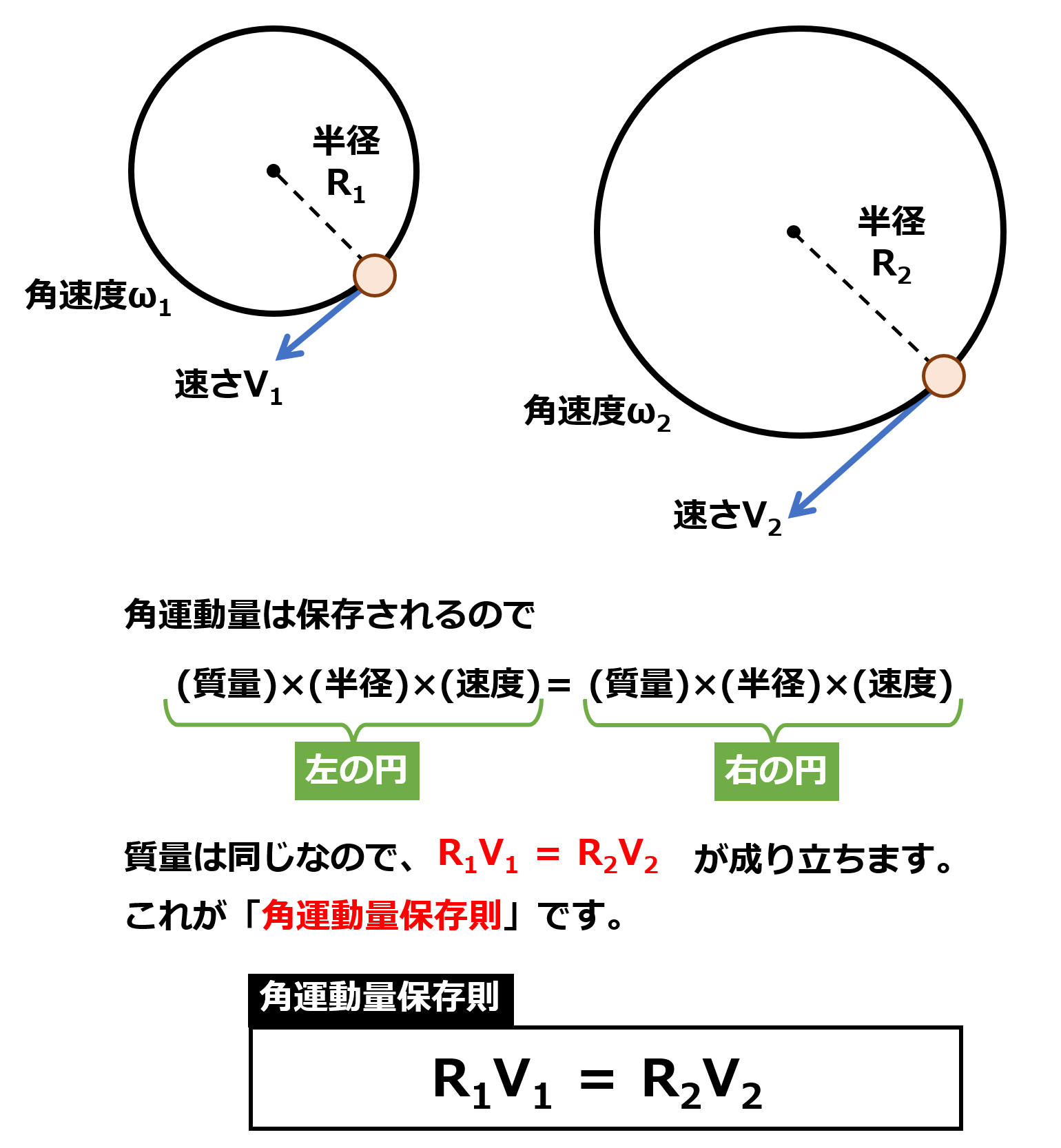
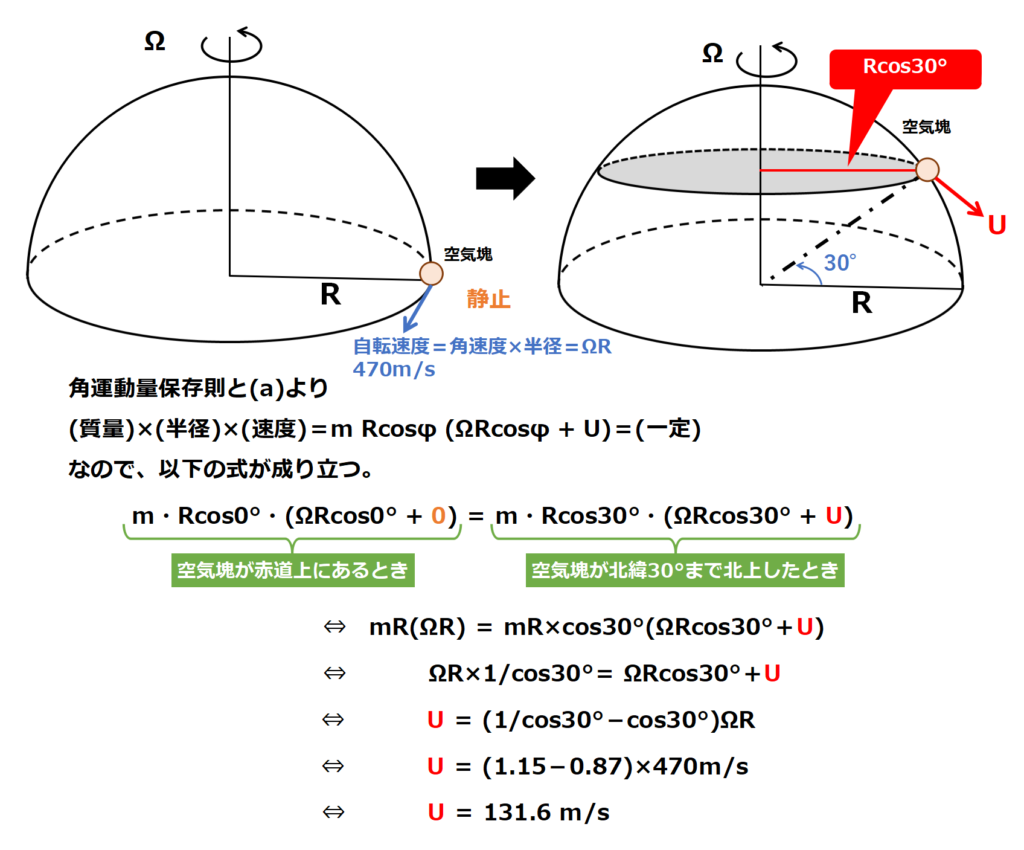
緯度φにあって，質量m，東⻄⽅向の速度U をもつ空気塊に対する⾓運動量保存則は，地球の半径と⾃転⾓速度をそれぞれR ，Ωとすると，(a) = ⼀定，と表現できる。
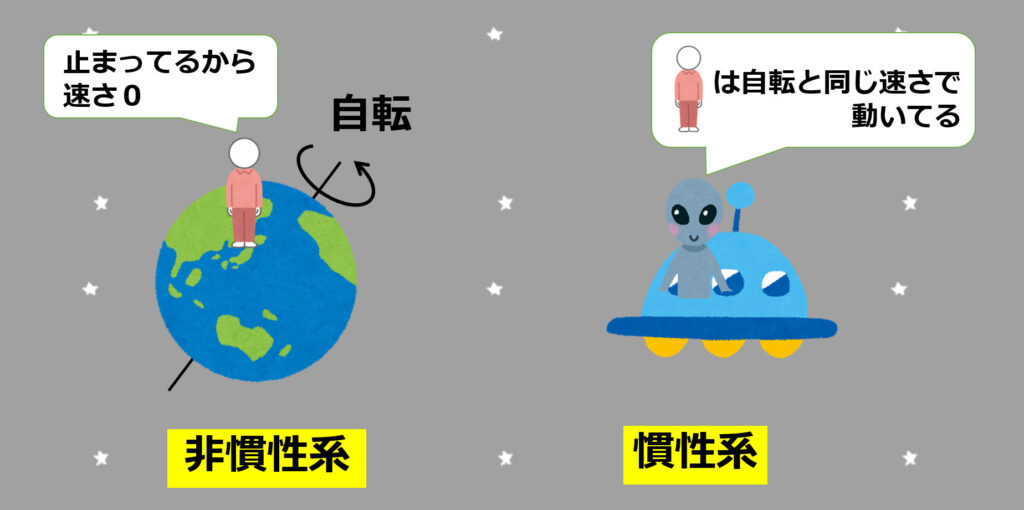
⾚道上空で地表⾯に対し相対的に静⽌していた空気塊が⾓運動量を保存しながら北緯30°まで北上した時の地表⾯に対する東⻄⾵速は，この式に基づくと約 (b) m/s となる。
| (a) | (b) | |
| ① | m R U | 60 |
| ② | m R (ΩRcosφ + U) | 60 |
| ③ | m R (ΩRcosφ + U) | 130 |
| ④ | m Rcosφ (ΩRcosφ + U) | 60 |
| ⑤ | m Rcosφ (ΩRcosφ + U) | 130 |
はじめに、角速度をおさえておきましょう。
次に角速度と速さの関係をみていきます。
最後に「角運動量保存則」の説明です。
「角運動量保存則」は「運動量保存則」がもとになっています。
運動量保存則は「物体の質量と速さの積(=運動量)は保存される」という法則です。
すなわち、運動量=(質量)×(速度)＝mv＝(一定)となります。
「角運動量保存則」は「運動量保存則」に半径を加えたもので、
角運動量＝(質量)×(半径)×(速度)＝mrv＝(一定)となります。
よって、以下2つの円について次のことが成り立ちます。
「角運動量保存則」は(質量)×(半径)×(速度)＝(一定)となる法則です。
よって、質量・半径・速度の3項目を考えていきます。
まず、問題文より質量は「m」です。
次に、半径を求めます。
地球の半径がR、緯度φにある空気塊では、以下のようになります。
よって半径は「Rcosφ」です。
最後に速度を求めます。
このときポイントとなるのは、空気塊が慣性系に対してどう動いているかを考慮することです。
慣性系と非慣性系の説明は以下の通りです。
・非慣性系・・・地球上の人から見た動き
地球上にいる人が動かずに止まっているとき、その人は自分が止まっていると認識します。
しかし、宇宙からその人を見た場合、地球の自転にあわせてその人は動いているように見えます。
このとき、宇宙から見た動きを「慣性系」、地球上にいる人から見た動きを「非慣性系」といいます。
角運動量保存則は慣性系についての運動法則です。
よって、地球上にある空気塊の動きを考えるときは、「空気塊の動き」に加えて「空気塊が地球の自転にあわせてどう動いているか」を考慮する必要があります。
問題文より、空気塊は速度Uで動いています。そのため「空気塊の動き」は「速度U」です。
これに、地球の自転による動きを考慮します。
地球の自転による動きの速度をVとすると、空気塊は半径Rcosφの円の上を動いています。
物体が円上を動くときの速さは(半径)×(角速度)なので、求めるべき空気塊の速度は以下の通りです。
よって速度は「ΩRcosφ + U」です。
これで質量・半径・速度の3項目がそろいました。
・質量は「m」
・半径は「Rcosφ」
・速度は「ΩRcosφ + U」
問題文より、(a)の答えは
(質量)×(半径)×(速度)＝m Rcosφ (ΩRcosφ + U)
です。
(b)では具体的に数字を使って⾵速を求めます。
よって(b)の答えは「130」です。