凝結過程による雲粒の成長
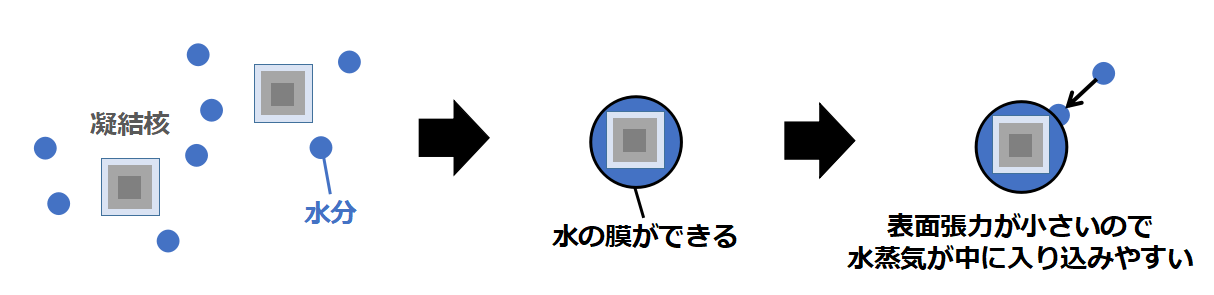
空気中に凝結核があると、それを核にして雲粒ができます。
凝結核は水を吸収しやすい性質があるので、空気中の水分を吸収して表面に水の膜を作ります。
小さい水滴の場合は表面張力が強くなりますが、「凝結核＋水の膜」はある程度の大きさがあるので、表面張力が弱くなって水蒸気が結合しやすくなります。
凝結核を元にして雲粒が生成し、雲が作られるようになると、凝結過程によって雲粒が成長します。
成長過程を式で表すと以下の通りです。
単位時間当たりの半径の増加量（dr/dt）は半径ｒに反比例することがわかります。
過飽和度を一定とすると、半径の小さい水滴ほど単位時間に半径が増大する割合は大きくなります。
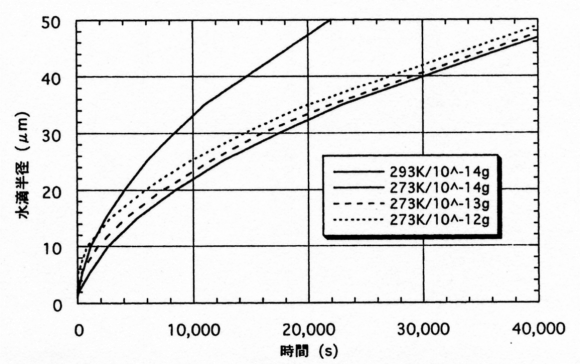
これをグラフにしたものが下図です。
水滴の凝結成長の計算例（雲と雨の気象学(水野量)）
よって雲粒は半径が小さいほど凝結成長が速いです。
「小さいほうが、すぐに沢山の水蒸気とくっついて速く大きくなる」というイメージができると良いでしょう。