数値予報とその予測対象である⼤気現象について述べた次の⽂章の下線部(a)〜(c)の正誤の組み合わせとして正しいものを、下記の①〜⑤の中から1 つ選べ。
⼤気現象には様々な時間空間スケ−ルを持つものがあるが、⼀般に、(a) 数値予報モデルで予測可能な現象の⽔平スケールの下限は、⽔平格⼦間隔が⼩さいほど⼩さくなる。
また、数値予報が予測できる⼤気現象は、数値予報モデルによっても異なる。数値予報において組織化された積乱雲からもたらされる強い降⽔の予測精度を向上させるには、(b) プリミティブ⽅程式系を基礎⽅程式とする数値予報モデルを⽤いる必要があり、物理過程として最も重要な部分は、(c) 地⾯からの蒸発や⽇射による地⾯の加熱を考慮した下部境界からの熱・⽔蒸気供給のパラメタリゼーションである。
| (a) | (b) | (c) | |
| ① | 正 | 正 | 誤 |
| ② | 正 | 誤 | 正 |
| ③ | 正 | 誤 | 誤 |
| ④ | 誤 | 正 | 正 |
| ⑤ | 誤 | 正 | 誤 |
③ a：正 b：誤 c：誤
「⼤気現象には様々な時間空間スケ−ルを持つものがあるが、⼀般に、(a) 数値予報モデルで予測可能な現象の⽔平スケールの下限は、⽔平格⼦間隔が⼩さいほど⼩さくなる。」
これは正です。
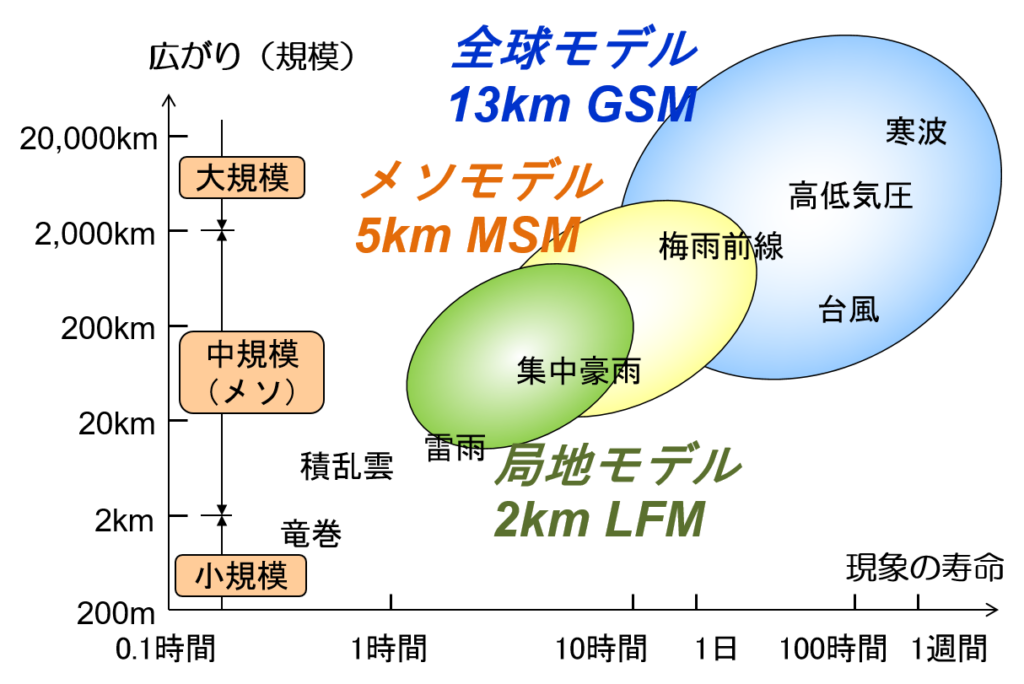
数値予報モデルで予測可能な気象現象の規模は、格子間隔の大きさに依存しています。格子間隔が小さいほど、モデルが表現できる最小の水平スケールは小さくなります。
・全球モデル（格子間隔：約13km）→水平規模が100km前後～の現象（高・低気圧、台風、梅雨前線など）
・メソモデル（格子間隔：5km）→水平規模が数10km以上～の現象（局地的な低気圧、組織化された積乱雲群など）
・局地モデル（格子間隔：2km）→水平規模が10数km程度の現象（組織化された積乱雲群など）※個々の積乱雲は難しい
「数値予報において組織化された積乱雲からもたらされる強い降⽔の予測精度を向上させるには、(b) プリミティブ⽅程式系を基礎⽅程式とする数値予報モデルを⽤いる必要があり、」
これは誤です。
プリミティブ⽅程式とは、数値予報で用いる物理学の方程式のうち、静⼒学平衡が成り立つと仮定した方程式です。つまり、鉛直方向に運動がない状態を仮定できるときに、利用することができます。
高気圧や台風、梅雨前線など、水平規模の大きい現象は、鉛直方向の運動は相対的に小さくなるため、静⼒学平衡が成り立つとみなすことができます。
そのため全球モデル（GSM）は、プリミティブモデルです。
一方、今回の問題の「組織化された積乱雲」は、メソモデル（MSM）あるいは局地モデル（LFM）の対象となる気象現象です。
メソモデルと局地モデルは「非静力学モデル」のため、”プリミティブ⽅程式系を基礎⽅程式とする数値予報モデル”ではありません。
| プリミティブモデル | 数値予報で用いる物理学の方程式の内、鉛直方向の運動方程式に静水圧近似を用いる数値予報モデルのこと。ＧＳＭはプリミティブモデルである。 |
| 非静力学モデル | 数値予報で用いる物理学の方程式の内、鉛直方向の運動方程式に静水圧近似を用いない数値予報モデルのこと。高い分解能で予報を行う場合、静水圧近似の精度が悪くなるので、非静力学モデルが必要である。ＭＳＭ、ＬＦＭは非静力学モデルである。 |
「数値予報において組織化された積乱雲からもたらされる強い降⽔の予測精度を向上させるには、（中略）、物理過程として最も重要な部分は、(c) 地⾯からの蒸発や⽇射による地⾯の加熱を考慮した下部境界からの熱・⽔蒸気供給のパラメタリゼーションである。」
これは誤です。「下部境界からの熱・⽔蒸気供給のパラメタリゼーションが最重要」とは言えません。
まず、パラメタリゼーションについてみていきます。
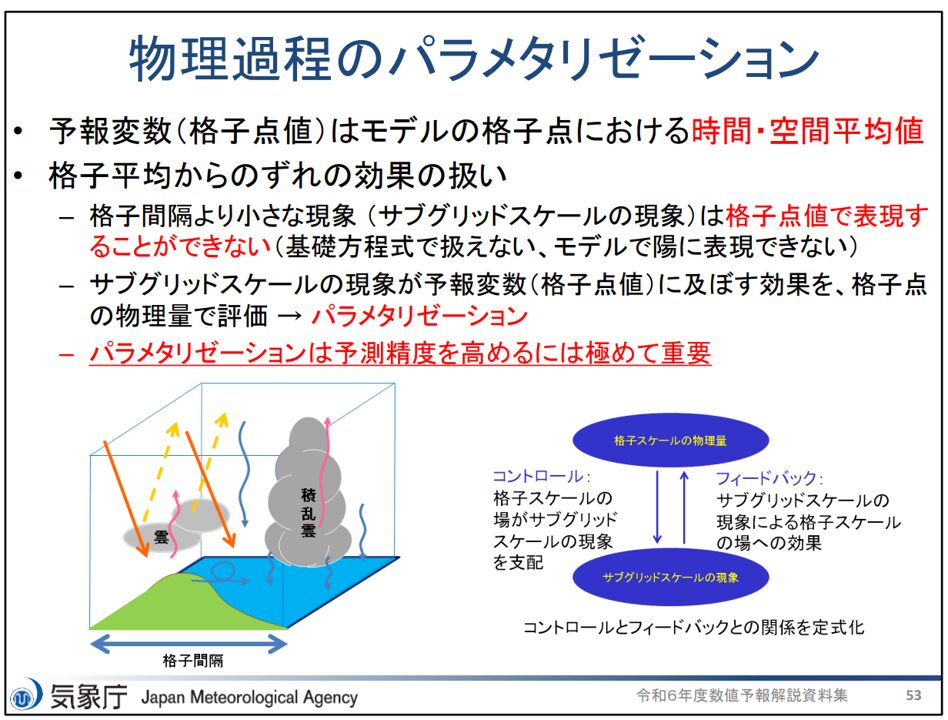
数値予報モデルでは、地球を細かい「マス目（格子点）」に分けて、そこでの気温・湿度・風などを計算します。このとき、格子点値（＝予報変数）は時間的・空間的な平均値を用いています。
しかし、雲の中の小さな動きや地面からの蒸発など、格子間隔より小さな現象（サブグリッドスケール現象）は、直接計算できません。
そこで、サブグリッドスケール現象が格子点値に及ぼす効果を、簡単な式やルールで近似して計算しています。これが「パラメタリゼーション」です。
パラメタリゼーションの結果は、格子平均からのずれの効果として、その格子点の値に取り入れられています。
数値予報で使われるパラメタリゼーションは様々ありますが、いくつか代表的なものを下表に示します。
| 物理過程 | 内容 |
|---|---|
| 積雲対流 | 積乱雲などの対流活動を近似的に表現。熱・水蒸気の鉛直輸送を扱う。 GSMで採用されているArakawa-Schubertスキームや、MSMとLFMで採用されているKain-Fritschスキームなど、さまざまな手法がある。 |
| 雲 | 格子点内に”部分的に雲がある”状態を表し、雲量を診断/予報する。 |
| 放射 | 太陽光や地球放射の吸収・反射・放出を近似的に計算。短波放射と長波放射を分けて扱う。雲の重なり方（オーバーラップ）も重要：ランダム／マキシマム／マキシマムランダム |
| 地表面 | 地面からの熱・水蒸気の供給を表現。植生や土壌の状態も考慮されている。 |
| 大気境界層 | 地表付近の乱流による運動量・熱・水蒸気の輸送を表現。 |
| 重力波抵抗 | 地形などによる小規模な重力波が風を減速させる効果を表現。全球モデルで導入、メソモデルでは直接解像されるため未導入。 |
今回の問題では、「数値予報において組織化された積乱雲からもたらされる強い降⽔の予測精度を向上させるには」とあります。
組織化された積乱雲による影響を考えたいとき、より重要となるのは「積雲対流」のパラメタリゼーションです。
積乱雲などの対流活動を、より正確に表現できれば、強い降⽔の予測精度向上も期待できます。
「下部境界からの熱・⽔蒸気供給のパラメタリゼーション」は、地表面や大気境界層のパラメタリゼーションを指しているため、最重要とは言えません。
参考：数値予報とは（気象庁） 、数値予報解説資料集（気象庁）、第4章 数値予報モデル（気象庁）、総観気象学 理論編（気象庁 監修、北畠尚子 著）
