図のように、地表面から鉛直に重なった高さH、H、2H の3 つの直方体の領域を考える。各直方体の東側と西側の面では、図に示す西風が各面内で一様に吹いている。各直方体の南側と北側の面を通過する風はなく、地表面以外の水平面 A、B、C では鉛直風が各面内で一様に吹いている。面A における鉛直風速が上向きを正として0.5m/s であるとき、面 C における鉛直風速として正しいものを、下記の①～⑤の中から 1 つ選べ。ただし、大気の密度はどこも同じで一定とする。
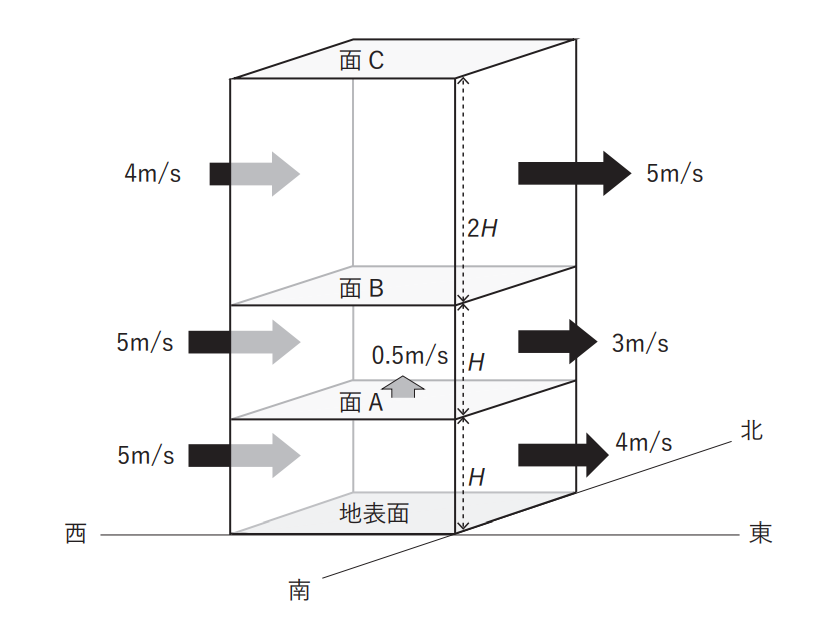
| ① | －1.0 m/s |
| ② | －0.5 m/s |
| ③ | 0 m/s |
| ④ | 0.5 m/s |
| ⑤ | 1.0 m/s |
④ 0.5 m/s
この問題は、質量保存の法則（連続の式）を使って鉛直風速を求める問題です。
まずは問題文から条件を整理しましょう。
条件
・東西方向の風速（西風）が与えられている。
・直方体の端から南北方向に吹く風はない。
・面Aの鉛直風速：+0.5 m/s（上向き）。
・大気密度は一定。
・求めるのは面C（最上層）の鉛直風速。
今回は空気の密度が一定なので、質量保存則より「流入量＝流出量」で考えることができます。
解答への考え方
・直方体の側面（東西面）からの風は、 水平方向の風速 × 面積 で求める。
・鉛直方向の風速は、水平面 A, B, C での鉛直流出入で表す。
・各直方体ごとに収支を計算する。
各層ごとに、「流入量＝流出量」を計算していきます。
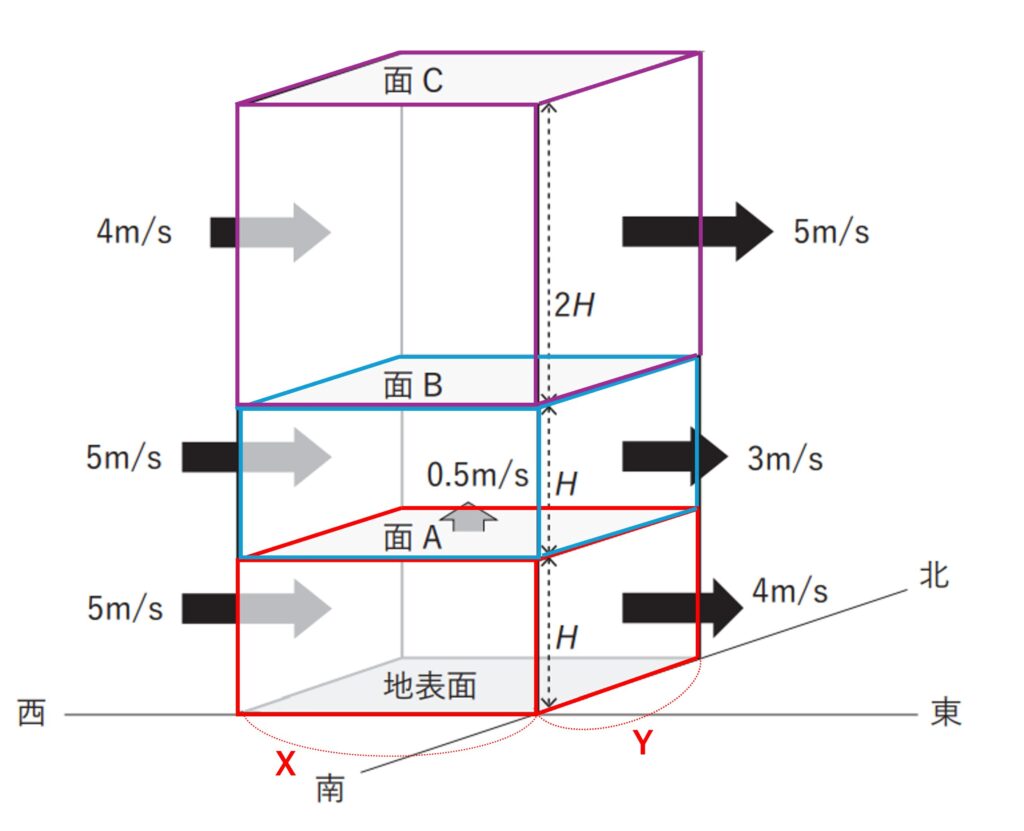
上記の計算は、プラスマイナスを気にせずに計算しました。
本問題では「鉛直風速が上向きを正」とするので、「面C（最上層）での流出＝上方向への風の流れ」で考えると、符号はプラスになります。
よって答えは「④ 0.5 m/s」です。
