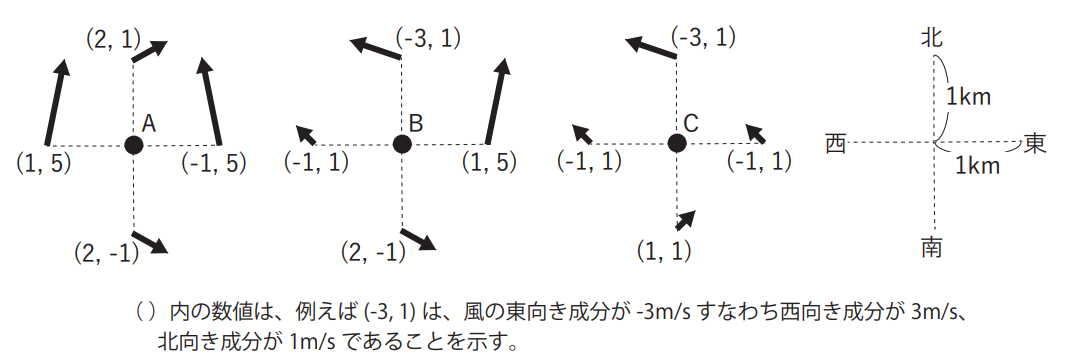
図のように北半球の同じ緯度の水平面上に●で示す3 つの点A、B、C があり、各点から東西南北に1km 離れた4 点で、矢印で示す水平風の風ベクトルが観測された。4 点に付した( )内の数値は(東向きを正とする風の東西成分[m/s],北向きを正とする風の南北成分[m/s])である。 点 A、B、C における渦度の鉛直成分を東西南北の4 点の水平風を用いて近似計算した値をそれぞれζA、ζB、ζCとするとき、これらの大小関係を表す式として正しいものを、下記の①~⑤の中から1 つ選べ。
| ① | ζA < ζB < ζC |
| ② | ζA < ζC < ζB |
| ③ | ζB <ζA <ζC |
| ④ | ζB < ζC < ζA |
| ⑤ | ζC < ζA< ζB |
② ζA < ζC < ζB
渦度とは、流体(空気や水など)がどれだけ回転しているかを示す量です。気象学では特に「風の流れの中での回転の強さ」を表す指標として使われます。
風が蛇行したり、風速が場所によって違っていたりすると、空気が回転するような流れが生まれます。この「回転の度合い」が渦度です。
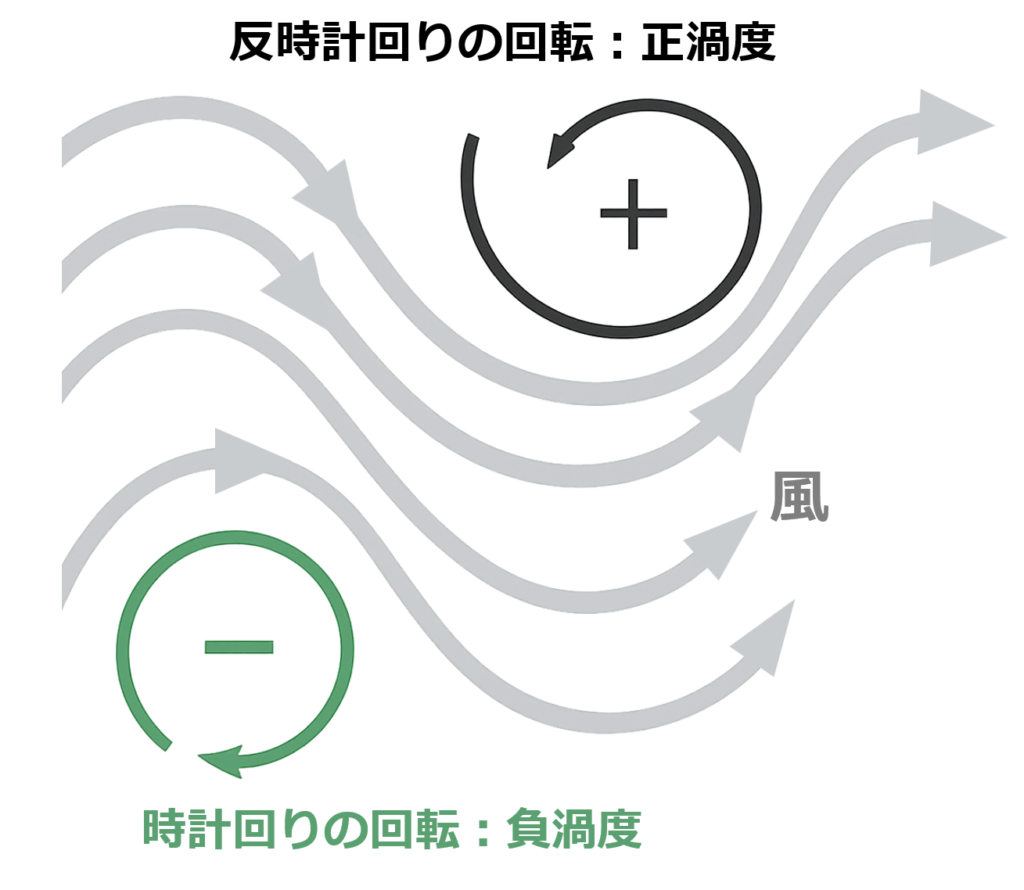
ちなみに、風がまっすぐ吹いているだけなら、渦度はゼロです。
天気図などで扱うのは、主に鉛直方向の渦度です。これは「鉛直軸(上向き)まわりの回転の強さ」を表します。
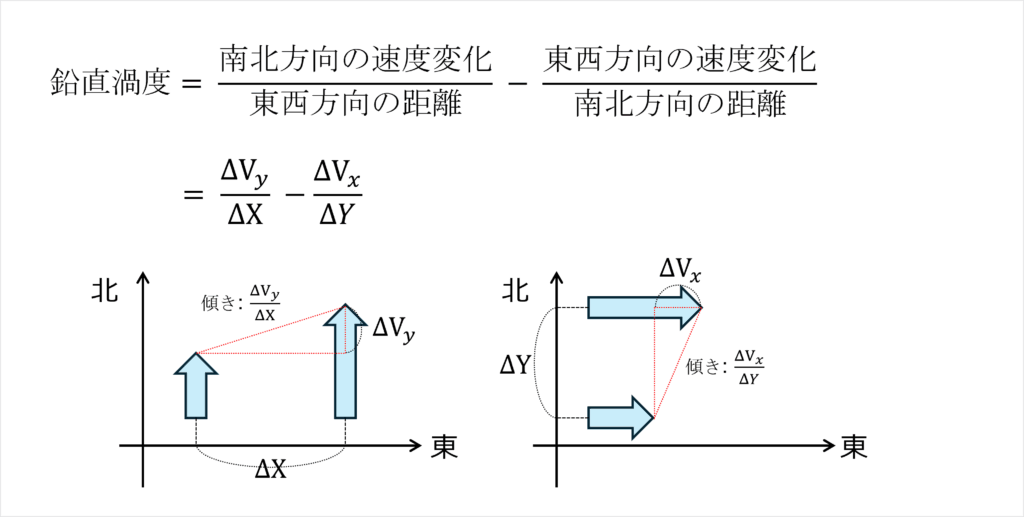
鉛直方向の渦度を求めるときは、
・南北風 が、東西方向にどれだけ変わっているか
・東西風 が、南北方向にどれだけ変わっているか
の2つを組み合わせて考えます。
上記の計算は、地表から見た「相対渦度」で考えていました。
しかし、地球は反時計回りに自転しているため、高気圧や低気圧といった総観場の事象を考えるときなどは、地球の自転の影響も考慮する必要があります。
地球の自転による渦度は「惑星渦度」と言います。
なお、地球の自転の影響をとりいれた渦度は「絶対渦度」です。相対渦度と惑星渦度の和が、絶対渦度になります。
・相対渦度:地表から見た風による回転の強さ。風のシアー(風速の差)や蛇行によって生じる。
・惑星渦度:地球の自転によって生じる回転の成分。緯度によって変化する。
・絶対渦度:相対渦度+惑星渦度。慣性系(宇宙から見た視点)での回転の強さ。
点 A、B、C における渦度の鉛直成分を求めてみましょう。
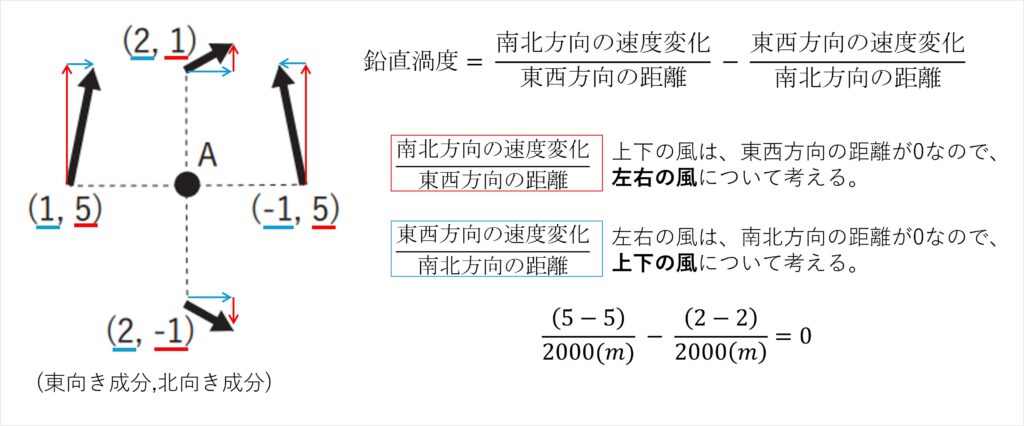
点 Aと同様に考えて、計算していきます。
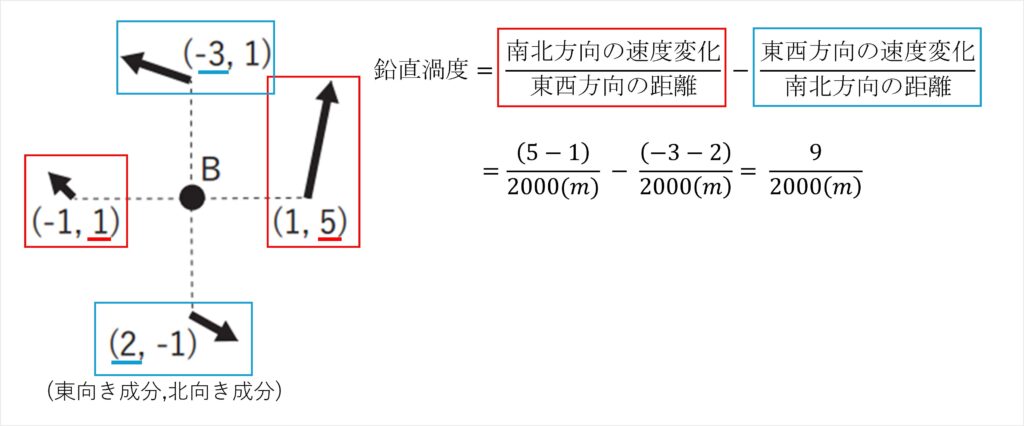

以上より「ζA=0、ζB=9/2000、ζC=4/2000」なので、大小を比較すると、「ζA < ζC < ζB」となります。
