大気中の点Aにおける気温変化について述べた次の文章の空欄(a)、(b)に入る数値の組み合わせとして適切なものを、下記の①〜⑤の中から1つ選べ。ただし、風速と水平方向の気温傾度はどこでも一様とし、sin30°=0.50、cos30°=0.87 とする。
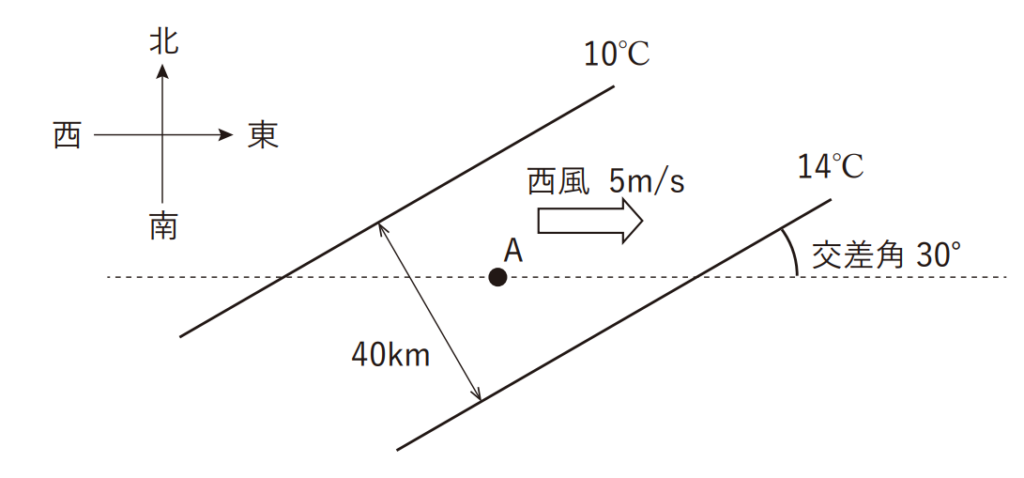
ある高度の水平面上で、図のように10℃と14℃の等温線が 40km の間隔で平行に並び、いずれも東西方向と 30° の角度で交差している。また、この水平面上では風速5m/s の西風が吹いている。このとき、2本の等温線の中間にある点Aにおける東西方向の気温傾度は、1kmあたり (a) ℃である。また、点Aにおける移流による気温の時間変化率は、1時間あたり (b) ℃である。
| (a) | (b) | |
| ① | 0.05 | −0.9 |
| ② | 0.05 | −0.25 |
| ③ | 0.087 | −1.6 |
| ④ | 0.1 | −1.8 |
| ⑤ | 0.1 | −0.5 |
① a:0.05 b:−0.9
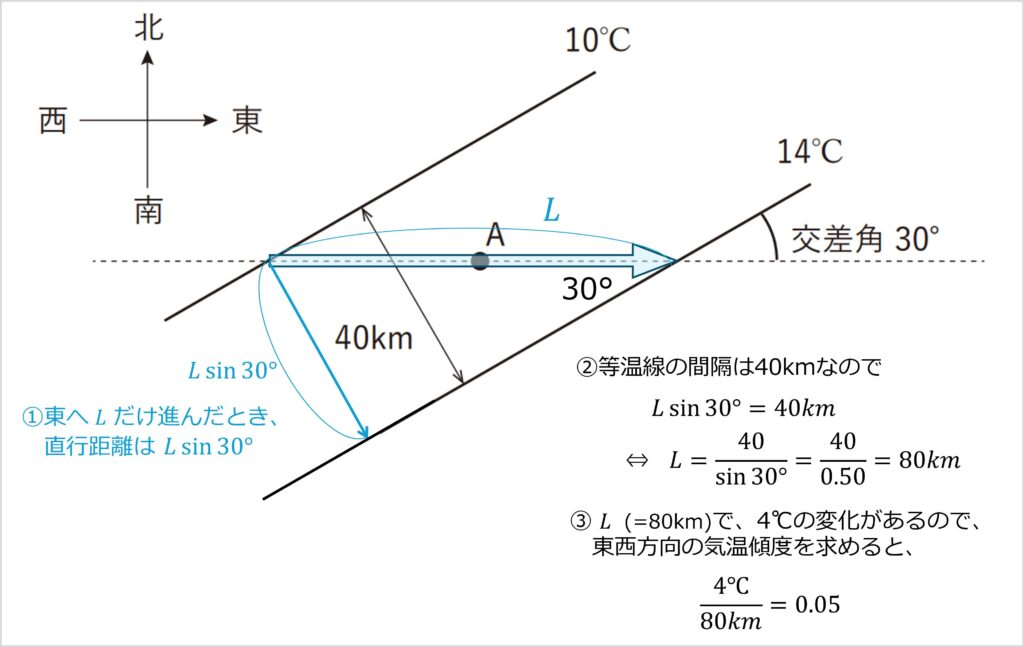
点Aにおける東西方向の気温傾度を求めます。
たとえば「気温が 20℃ の場所」に立っているとします。
・もし風が「10℃ の冷たい場所」から吹いてきたら、だんだん冷たい空気に入れ替わって気温は下がる。
・逆に「30℃ の暖かい場所」から風が来たら、だんだん暖かくなって気温は上がる。
これが「移流による気温変化」です。
・傾度 = 1 km 進むと何℃変わるか
・風速 = 何 km/h で空気が運ばれてくるか
・掛け算すると、「1時間あたりにどれだけ温度が変わるか」が出る
点Aでは、西風 5 m/s が吹いています。単位を直すと、5 m/s は 18 km/h です。
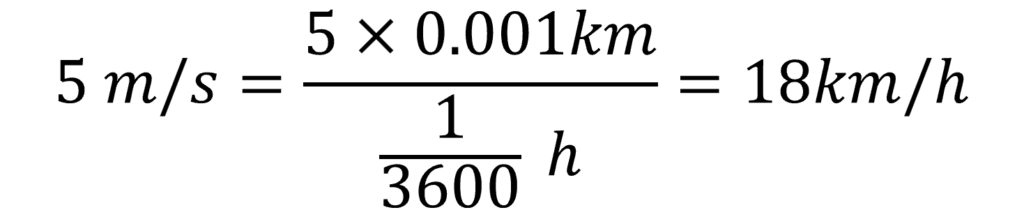
本問題での情報をまとめると、以下のようになります。
・点Aにおける東西方向の気温傾度:0.05 ℃/km(東に1 km 進むと 0.05 ℃上がる)
・点Aでの風速:18 km/h(18 km離れた西の空気が1時間で運ばれてくる)
「傾度×風速=気温変化」なので、
0.05℃/km × 18 km/h = 0.9 ℃/h
点Aでは西風なので、等温線の10℃→14℃に向かって風が吹いています。
そのため西風 5 m/s (18 km/h)が吹くと、点Aにおける気温は下がります。
よって(b)の答えでは、符号がマイナスになるので、「-0.9 ℃/h」です。
本記事に掲載している試験問題は、「一般財団法人 気象業務支援センター」様の許可を得て使用しています。
解説は当サイト運営者が独自に作成したものであり、同センターとは一切関係ございません。
なお、本記事の内容に基づいて生じた損害等について、当サイトは責任を負いかねますのでご了承ください。