次に⽰す 3 種類の湿潤空気塊の⽐湿 A、B、C の⼤⼩関係として正しいものを、下記の①〜⑤の中から1つ選べ。ただし、⽐湿sは、⽔蒸気圧e、気圧pを⽤いて、s = 0.622e /pで近似できるものとする。また、温度と飽和⽔蒸気圧の関係は次の表の通りとする。
| 温度（℃） | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 |
| 飽和水蒸気圧（hPa） | 12 | 14 | 16 | 18 | 21 | 23 | 26 | 30 | 34 | 38 | 42 |
A 温度12℃の乾燥空気990g と⽔蒸気10g からなる湿潤空気塊の⽐湿
B 温度14℃、相対湿度75 %、気圧700hPa の湿潤空気塊の⽐湿
C 温度20℃、露点温度16℃、気圧900hPa の湿潤空気塊の⽐湿
| ① | A < B < C |
| ② | A < C < B |
| ③ | B < A < C |
| ④ | B < C < A |
| ⑤ | C < A < B |
① A < B < C
はじめに、乾燥空気と湿潤空気について押さえておきましょう。
比湿とは、乾燥空気1kgあたりに含まれる水蒸気の質量（kg）です。
たとえば、乾燥空気が1kgあって、そこに0.01kg（=10g）の水蒸気が含まれていたら、比湿は0.01となります。
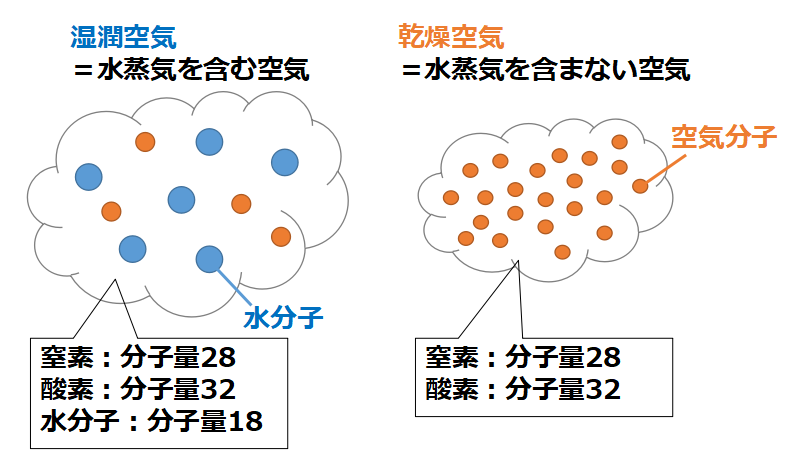
気温が高くなると空気は膨張するので体積は変わりますが、「質量（gやkg）」は、気体が膨張・収縮しても変わらない物理量です。
そのため、気温が変わっても、空気の水蒸気量が変わらなければ、比湿は一定となります。
問題文に「⽐湿sは、⽔蒸気圧e、気圧pを⽤いて、s = 0.622e /pで近似できるものとする」とあるように、比湿は圧力を用いて計算ができます。これは、理想気体の法則により、質量を圧力から間接的に計算できるからです。
この式について、詳しく見ていきましょう。
まず、理想気体の状態方程式を用いて質量を表すと、以下のようになります。
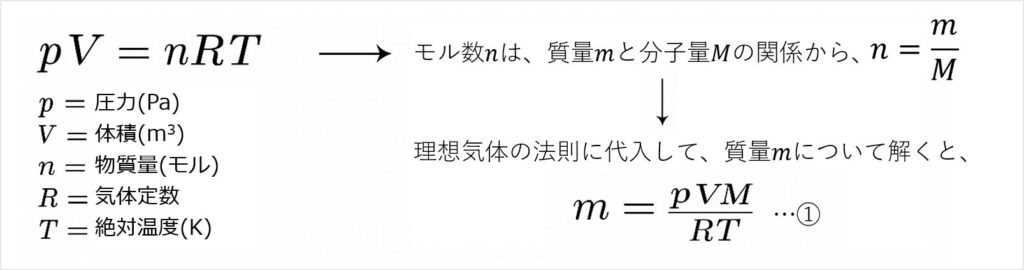
水蒸気（湿った成分）と乾燥空気は、別々の理想気体として考えることができます。理想気体の状態方程式から、水蒸気と乾燥空気のそれぞれの質量を算出して、比湿を求めてみます。
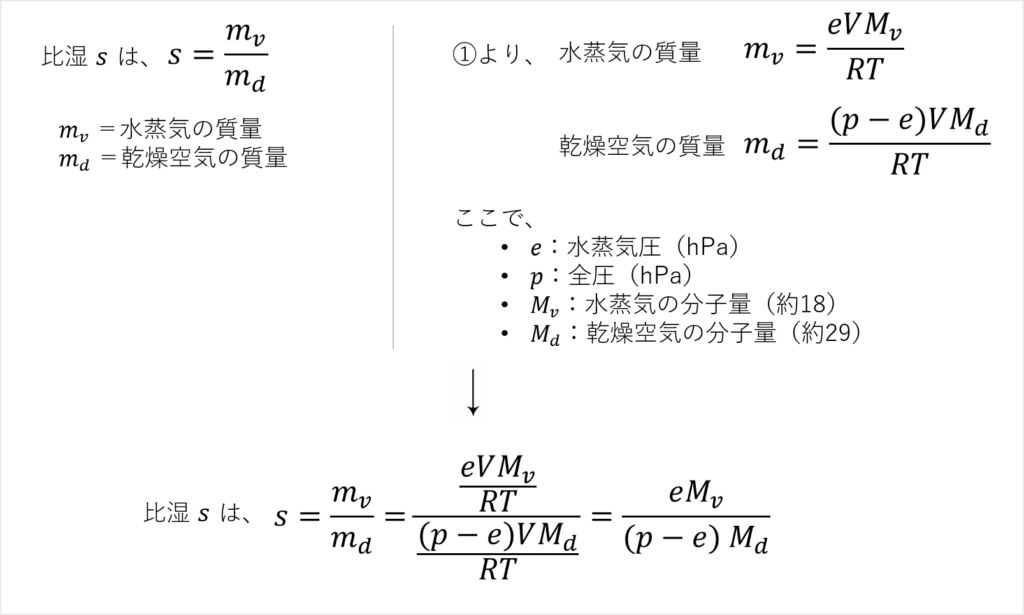
大気中では、⽔蒸気圧eは通常1～40hPaです。
一方、気圧（全圧）pは約1000hPaです。天気図でも1000hPa前後の気圧を見ることが多いと思います。
そのため、（p－e）≒ p と近似することができます。
よって比湿sは、以下のようになります。
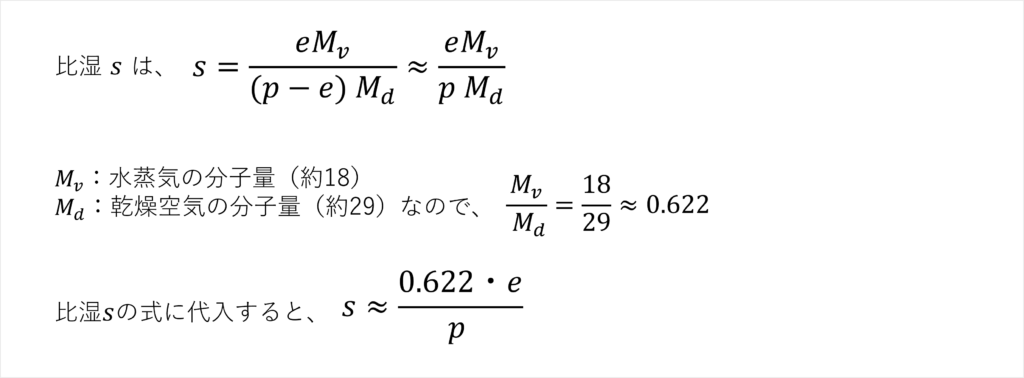
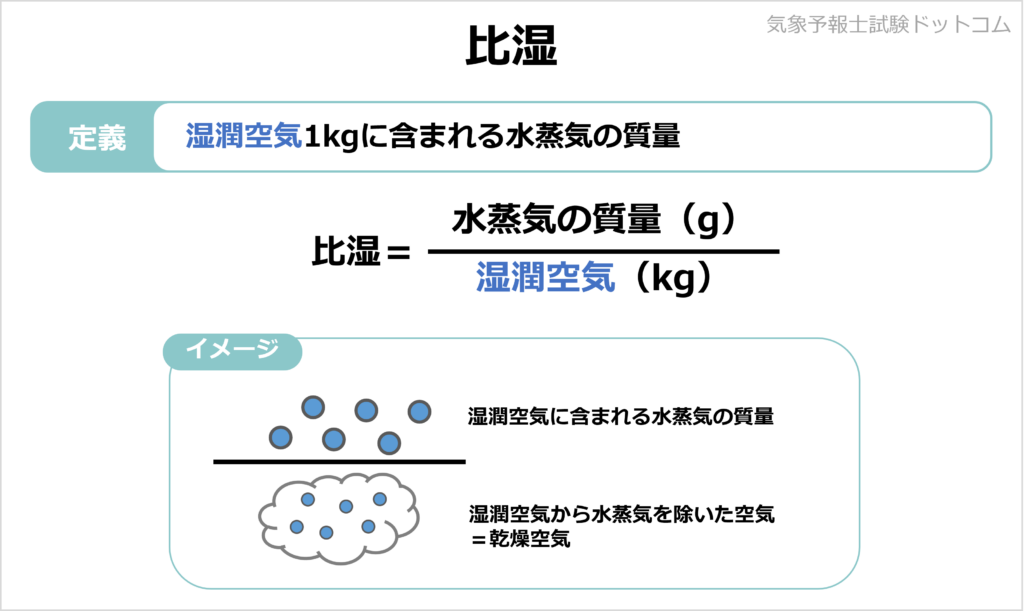
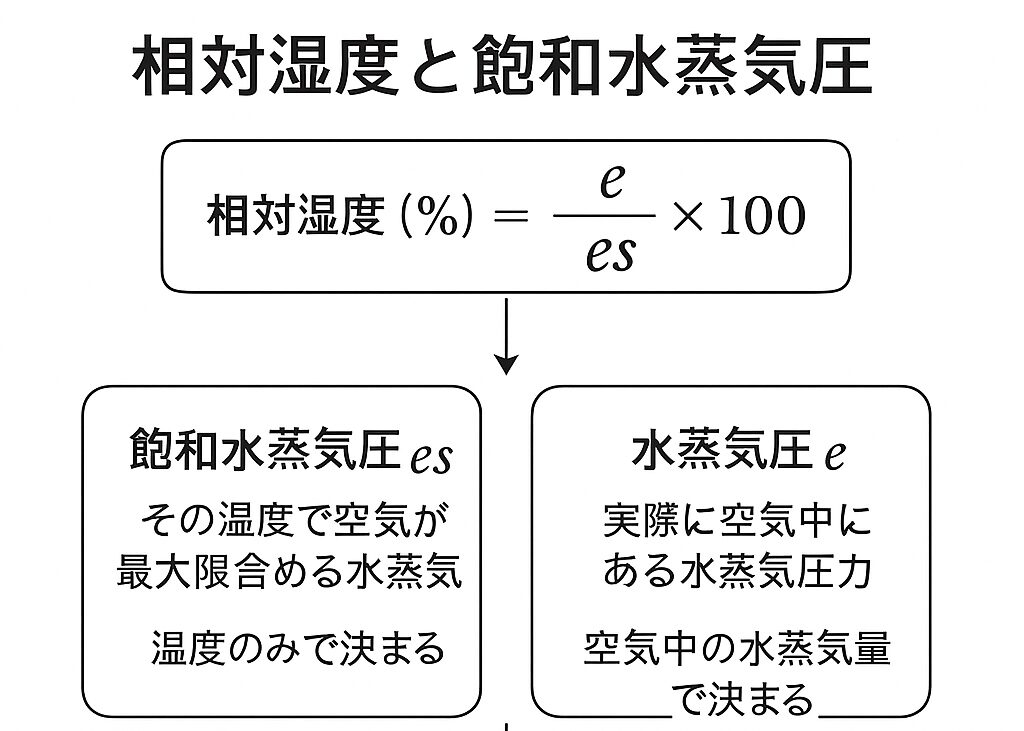
相対湿度とは、ある空気に含まれる水蒸気の割合です。
空気は温度によって含むことのできる水蒸気量が決まっていて、含むことのできる水蒸気量の最大が「飽和水蒸気量」です。
また、水蒸気量ではなく水蒸気圧の割合に置き換えることもできます。
つまり、以下の式で表すことができます。
「温度12℃の乾燥空気990g と⽔蒸気10g からなる湿潤空気塊の⽐湿」を求めていきます。
比湿とは、乾燥空気1kgあたりに含まれる水蒸気の質量なので、乾燥空気と水蒸気の質量がわかれば比湿を求めることができます。
Aでは「乾燥空気990g と⽔蒸気10g 」とあるので、単純にこれらの数字を用いて計算します。
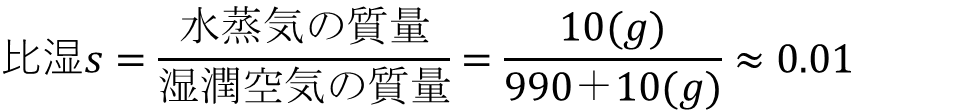
「温度14℃、相対湿度75 %、気圧700hPa の湿潤空気塊の⽐湿」を求めていきます。
Bでは、乾燥空気と水蒸気の質量が書かれていません。ただし、問題文より、水蒸気圧と気圧がわかれば比湿は計算できることがわかります。
気圧は700hPaとあるので、「温度14℃、相対湿度75 %」の情報から水蒸気圧を求めていきます。
問題文の表から、温度14℃の飽和水蒸気圧は16hPaとわかります。
いま、Bの空気は相対湿度75 %なので、水蒸気圧は以下のように求められます。
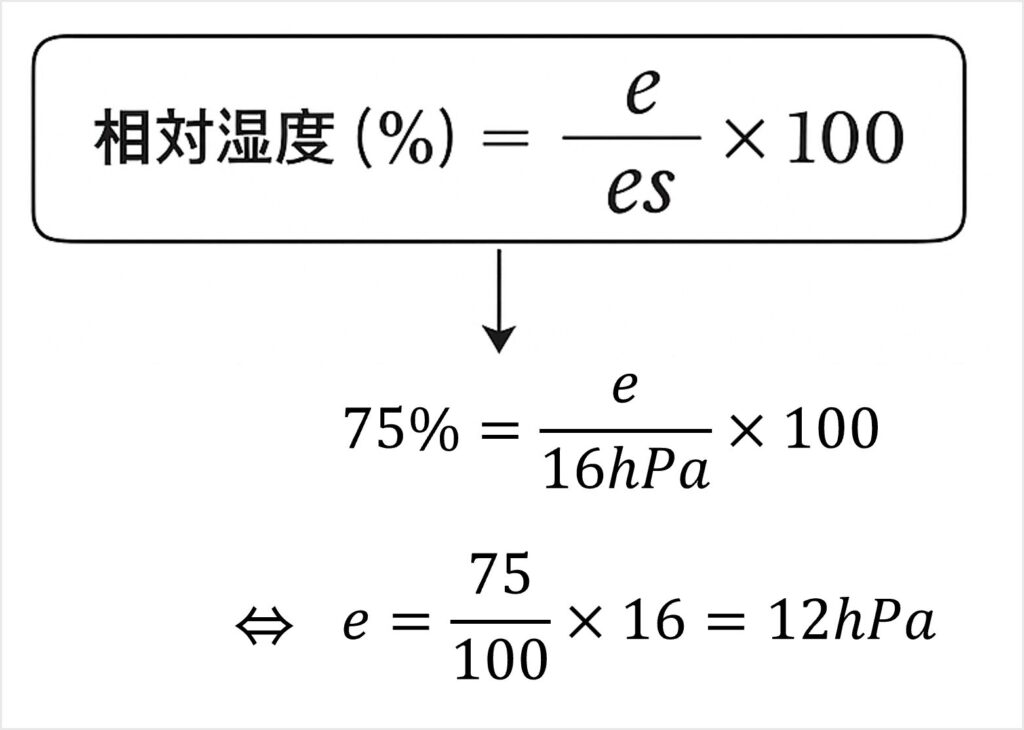
気圧は700hPa、水蒸気圧は12hPaなので、問題文の式から比湿を求めます。
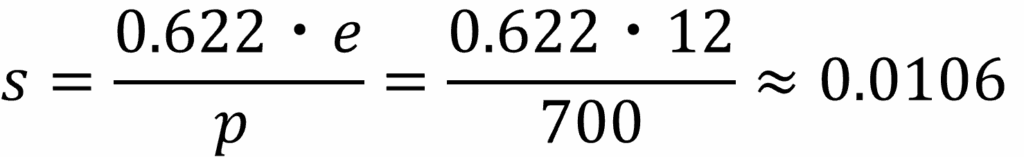
「温度20℃、露点温度16℃、気圧900hPa の湿潤空気塊の⽐湿」を求めていきます。
気圧は900hPaとあるので、「温度20℃、露点温度16℃」の情報から水蒸気圧を求めましょう。
まず、露点温度とは、空気を冷やしていったとき、水蒸気が飽和し始める温度です。
Cの空気は、露点温度が16℃なので、温度20℃の状態では飽和していません。20℃から冷やしていき、16℃に達すると、水蒸気が飽和して凝結し始めます。
「露点温度」での水蒸気圧が、今その空気に実際に含まれている水蒸気量を示しているので、問題文の表から温度16℃の飽和水蒸気圧を確認すると18hPaとわかります。
気圧は900hPa、水蒸気圧は18hPaなので、問題文の式から比湿を求めます。
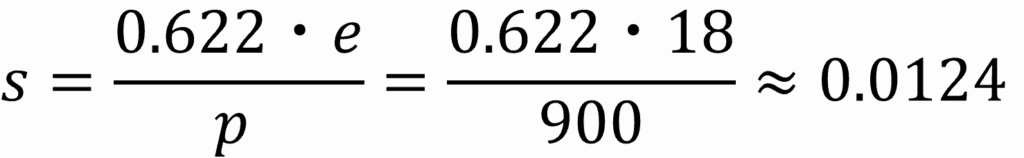
よってA～Cの比湿は、A：0.0101、B：0.0106、C：0.0124なので、問題の回答は「A < B < C」だとわかります。
